2D points 3D Objects 3D Points Boundary Cursor position Data for selected object Domain Expansion Field Field components Field formula Field tubes Function Generate expansions along 2D boundary Generate expansions for 3D objects Grid formula Grid transformation Info and movie directives Insert Integral Modify 2D expansions MMP Movie Open GL window PET basis PFD (predefined FD) Project Space, plane, arrow, or point Tools and draw Transformation data Window
Press the project button ![]() or
select Project... from the Tools menu to
open this dialog.
or
select Project... from the Tools menu to
open this dialog.
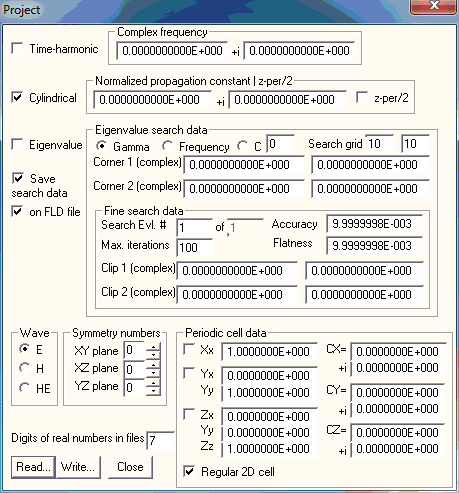
In the Project dialog, you specify the main data of a project. OpenMaXwell contains several tools for computing the field of a project, but not all tools can be used for solving all kind of problems. For example, only MMP can solve eigenvalue problems, but the MMP version implemented in OpenMaXwell cannot solve problems that are not time-harmonic. Moreover, not all of the data in this dialog needs to be specified for most projects. For example, the data in the Eigenvalue search data group is only used by MMP when the Eigenvalue box is checked. When using the GFD tool, much of the data specified in this dialog is redundant.
The additional box Digits of real mantissa in files allows you to specify the accuracy of real numbers stored in the various ASCII files of OpenMaXwell. The default value is 7. Especially, when ill-conditioned matrices occur, it may be reasonable to increase this value. When it is bigger than 10, the Fortran * format is used for writing the data files. This corresponds to the maximum accuracy and causes considerably longer ASCII files. If you think that the MMP matrix is ill-conditioned, you can save all data with a reduced accuracy, read the entire project again, and recompute the field without recomputing the amplitudes of the MMP expansions. In this field computation, the reduced accuracy of the parameters of the MMP expansion will reduce the accuracy of the field computation. If the field computation is worse than before, this is caused by the ill condition. Very ill-conditioned matrices require a data precision of more than 7 digits.
In case of periodic symmetries with more than one direction, the y period direction must not be perpendicular to the x period, i.e., it must not coincide with the y direction of the global coordinate system anymore, but it must be within the xy plane, i.e., the “y” period direction is defined by a vector in the xy plane. Moreover, a third “z” period direction has been introduced that is defined by an arbitrary vector in 3D space. In addition to that, the eigenvalue search has been improved as follows: 1) Up to 100 minima found during the rough search are temporarily saved. Therefore, it is sufficient to run the rough search only once before the fine search is started for the first 100 eigenvalues (using the directive “INCrease EIGenvalue” or by manually running MMP several times for different eigenvalues). This also holds when you modify the frequency for obtaining the frequency dependence of an eigenvalue – provided that you reset the frequency to the value it had during the rough search as soon as you switch to another eigenvalue. 2) A rectangular clip area in the complex eigenvalue search plane has been introduced. The fine search stops as soon as it runs outside the clip area. This feature is useful when you trace, for example, the frequency dependence of an eigenvalue and want to plot ist within a certain window. Moreover, it allows you to clip “forbidden” regions. For example, when you compute the propagation constant of guided modes, the second and fourth quadrant of the complex gamma plane are forbidden and you should restrict the search to the first quadrant. The Project dialog has been modified accordingly:
Check the Time-harmonic box, when your project is time-harmonic, i.e., when you work in the frequency domain, and specify the real and imaginary parts of the frequency in the Complex frequency group. Note that the original fields become complex in this case. The PFD solver is an FDTD even when the Time-harmonic box is checked. In this case, it will perform discrete Fourier transforms for each field point specified in the Field dialog. Therefore, you will obtain a complex time-harmonic field as from a frequency domain solver.
When the Time-harmonic box is not checked, OpenMaXwell works in the time domain. The PFD solver then uses the Complex frequency. for modulating the specified time dependence. Note that the original fields become real in this case and that the OpenMaXwell MMP implementation is unable to solve such problems, except for static problems with zero frequency.
Set the frequency to zero for static problems. There are two ways of approaching a static MMP problem.
When you check the Time-harmonic box, the original field is complex. Otherwise, it is real, which requires less memory. The former makes sense when you want to embed a static result into a dynamic computation as an approximate, quasi-static solution.
Static problems often have no explicit excitation. In such cases, a dummy excitation, i.e., a last expansion with a single parameter equal to zero, must be defined.
PFD contains simple iterative finite difference schemes for handling static problems.
When floating electrodes with known total charges are present, the total charges of these electrodes play the role of the excitation for the MMP tool. The total charge of each floating electrode is then modeled by a single monopole expansion with origin in the center of the electrode and the minimum orders of all multipoles in such an electrode are set equal to one. When more than one floating electrode is present, all monopoles in these electrodes must be embedded in a connection that is the excitation of the problem.
Check the Cylindrical box when the geometry of your problem is cylindrical and can be completely specified by the geometry of the cross section in the xy plane. Note that z is assumed to be the cylindrical axis. When the z-per/2 box is not checked, the propagation of time-harmonic waves along the z axis is specified in the Normalized propagation constant | z-per/2 boxes. Its real and imaginary parts are contained in the left and right box respectively. The propagation constant is equal to the normalized propagation constant times the free-space wave number. When the z-per/2 box is not checked, the half length of the period along the z axis is contained in the first of the Normalized propagation constant | z-per/2 boxes. Since z-per/2, i.e., half of the period in the z direction is a real value, the imaginary part is ignored. Note that the specification of z-per/2 is important for resonator problems. It may also be used for loss-free waveguide problems, but not for lossy waveguides.
When the Cylindrical box is not checked, the problem is assumed to be entirely 3D. You may also solve 3D problems with analytical formulae definition or with appropriate PFD schemes.
OpenMaXwell’s MMP tool supports problems that are 1) periodic in the x direction, 2) periodic in the x direction and a direction in the xy plane, 3) periodic in the x direction, a direction in the xy plane, and an arbitrary direction inxyz space. This means that you may have up to three periodic direction vectors. The first of them is in x direction, the second one within the xy plane, and the third is arbitrary. The first vector has the components (Xx,0,0); the second vector has the components (Yx,Yy,0); and the third vector has the components (Zx,Zy,Zz). All components may be specified in the corresponding boxes of the Periodic cell data group. Since all periodic problems can be defined in such a way that all components are positive, the priodic feature has only been tested for positive components of the periodic vectors. Therefore, it is reccomended to select the coordinate system in such a way that all components are positive. Check the corresponding X, Y , and Z boxes if the problem is periodic in the direction of the coressponding vector. Note that the X box must be checked when the Y box shall be checked and that the Y box must be checked when the Z box shall be checked. Furthermore, Z periodicity makes sense for 3D problems only. The Yx, Zx, and Zy components may be zero, but the Xx, Yy, and Zz components must be non-zero.
For each direction you can specify a complex factor Cx, Cy, and Cz. When any field component F has a (complex) value F(X,Y,Z) in an arbitrary point (X,Y,Z) of the 3D space, the corresponding value in the neighbor points (X+Xx,Y,Z), (X+Yx,Y+Yy,Z), (X+Zx,Y+Zy,Z+Zz), will be F(X+Xx,Y,Z)=F(X,Y,Z)*exp(i*Xx*Cx), F(X+Yx,Y+Yy,Z)=F(X,Y,Z)*exp(i*Abs(Yxyz)*Cy), F(X+Zx,Y+Zy,Z+Zz)=F(X,Y,Z)*exp(i*Abs(Zxyz)*Cz) respectively, where Abs(…) denotes the length of the correspondic periodic direction vector.
For gratings that are illuminated by a plane wave, OpenMaXwell computes the correct values for you. For waveguide structures that are periodic in X direction, you can consider Cx as the propagation constant that is an eigenvalue to be searched. In this case, check the Cx box in the Eigenvalue search data group and enter the search area in this group. Once the search has found a Cx value, OpenMaXwell will display it in the Cx box of the Periodic cell data group.
For any periodic problem, you should specify only the boundaries and expansions for the oricinal cell. This cell is defined as follows: 1) When only X symmetry is present, the cell starts at the plane X=0 and ends at X=Xx when the Regular 2D cell is checked. In the plane X=Xx, you should define an appropriate periodic boundary, whereas no boundary must be defined at X=0 because the periodic boundary at X=0 is automatically (implicitely) generated by moving the boundary at X=Xx with the negative of the first periodic vector. When the Regular 2D cell is not checked you may also specify a curved periodic boundary (2D problems only!) that is implicitely moved with the negative of the first periodic vector. In this case, the oricinal cell is a curved stripe. 2) When X and Y symmetries are present, and the Regular 2D cell is checked, you should define two periodic boundaries. The first one is X periodic and should contain the points X=Xx and (X,Y)=(Xx+Yx,Yy). The second one should be Y periodic and should contain the points (X,Y)=(Xx+Yx,Yy) and (X,Y)=(Yx,Yy). For 2D applications, you may also define curved periodic boundaries, when the Regular 2D cell is not checked. In this case, the X periodic boundary must start at X=Xx and end at (X,Y)=(Xx+Yx,Yy), whereas the Y periodic boundary must start at (X,Y)=(Xx+Yx,Yy) and end at (X,Y)=(Yx,Yy). 3) When X, Y, and Z symmetries are present, you must define a 3D model with at least three plane objects defining the three periodic boundaries. Defining such models is quite demanding!
In this version of OpenMaXwell, only the MMP tool is able to solve eigenvalue problems. There are two types of eigenvalue problems that can be solved: 1) guided waves on cylindrical structures and 2) 2D and 3D resonators. These two types are closely related and are computed using the same procedures. Either the propagation constant Gamma or the Frequency must be searched for. Select the desired search variable in the corresponding box. When gamma is the search variable, the frequency is a fixed parameter during the search and vice versa. For 3D resonators, gamma is not used.
For periodic structures, you can search for the CX, CY, CZ value or combinations of them: Check the C box and enter an integer number that defines which of the constants is searched for: 1: CX, 2: CY, 3: CZ, 4:CX=CY, 5:CX=CZ, 6:CY=CZ, 7:CX=CY=CZ. For example, for a periodic waveguide in x direction, select C1. CX=CY=CZ means that the three constant obtain equal values, all of them defined by the complex eigenvalue search (within the rectangular area defined by Corner 1 and Corner 2 (see below). Note that selecting C only makes sense when the corresponding periodic symmetry is specified in the Periodic cell data group. It is only possible to specify Z periodic symmetry when also Y periodic symmetry is selected. Y periodic symmetry requires X periodic symmetry to be specified. C1 corresponds to Cx in the older OpenMaXwell versions.
In general, the eigenvalue search variable is complex. The corresponding search space is a rectangle in the complex plane. The real and imaginary parts of two opposite corners of this rectangle may be specified in the corresponding boxes of the Eigenvalue search data group.
The rough search in the rectangular search area (defined by the lower left Corner 1 and the upper right Corner 2 in the comlex plane) is performed on a regular grid. The number of grid lines in the real and imaginary directions can be specified in the two Search grid boxes. MMP associates a real function to the search space and searches for the minims of this function. An eigenvalue is detected when the values of the four closest neighbors of a grid point are bigger than the value in the grid point itself. Note that the rough search is extremely time consuming when the number of grid lines is large, however the search might miss some minimums when only a small number of grid lines is specified.
When the number of lines in the imaginary direction is less than two, a rough search along a line from the first to the second corner of the search space is performed. This method is especially useful for loss-free cases with a real valued eigenvalue, for evanescent modes with an imaginary eigenvalue, and when either the real or the imaginary part of the eigenvalue is known or can be estimated.
When the number of lines in the imaginary direction is equal to one, the fine search will run in the complex plane. When it is zero, the fine search runs either parallel to the real axis or parallel to the imaginary axis. The latter is useful when you know that the eigenvalue is on the real axis (loss-free guided waves) or on the imaginary axis (evanescent waves of loss-free structures).
When the number of grid lines in the real direction is less than three, the rough search is suppressed and it is assumed that the eigenvalue is located in the middle between the two corners of the search space. This is useful when you have a good estimate of the eigenvalue to be searched, for example, from a previous eigenvalue search. Note that you should select the corners of the search space as close to the eigenvalue as possible, but in such a way that the eigenvalue is guaranteed to be in the search space. Otherwise, the search might fail.
In the Fine search data group you specify which of the eigenvalues detected in the rough search that the fine search should look for, the maximum number of fine search iterations to be performed, and two stopping criteria. This data is contained in the Search Evl., Max. iterations, Accuracy, and Flatness boxes. The fine search is stopped 1) when the relative accuracy is obtained, 2) when the function is too flat to obtain the desired accuracy, or 3) when the allowed number of iterations has been performed. The fine search is also stopped when it runs outside the clip area (defined by the lower left Clip 1 corner and the upper right Clip 2 corner in the complex plane).
Check the Save search data box when you wish to save the search data to a file. OpenMaXwell writes the rough search data to a field data file when the search is performed in a rectangle, i.e., when there are more than 2 gridlines in the real direction and more than 1 grid line in the imaginary direction are present. OpenMaXwell writes the search data to a function file when there are more than 2 grid lines in the real direction and less than 2 grid lines in the imaginary direction, i.e., when the rough search runs along a line. Moreover, OpenMaXwell saves the fine search data to a function file. This allows you to view the eigenvalue search space and the fine search behavior.
When you run the eigenvalue search from the MMP dialog, OpenMaXwell displays a file name dialog that allows you to specify a name for the search data files. When you run the search with the directive “MMP SOLve”, the current file name for search data files is used. To avoid overwriting, the number of this file is automatically incremented. When the file number exceeds 999, it is reset to 000.
In some problems, the field components can be either symmetric or anti-symmetric with respect to one of the three main planes XY, XZ, YZ. If this is the case, the computation time can be significantly reduced by taking the symmetry into account. To do this set the symmetry numbers of these planes in the corresponding boxes. The meaning of the symmetry numbers is as follows:
0: no symmetry,
1: on the symmetry plane, the E field is parallel and the H field is perpendicular,
2: on the symmetry plane, the H field is parallel and the E field is perpendicular.
Note that only the MMP tool takes symmetry planes into account. No symmetries may be used for periodic problems because this would require a more sophisticated symmetry decomposition that has not been implemented. Users of the former 3D MMP implementation (the 3D electrodynamic wave simulator) should notice that the symmetry number 3 is not valid in OpenMaXwell.
In the MMP computation of 2D problems, the wave type plays an important role. You may specify E, H, and HE waves in the corresponding boxes. For E waves, the longitudinal component Hz of the H field is zero, for H waves, the longitudinal component Ez of the E field is zero, whereas for HE and EH waves, all field components are non-zero in general. Note that OpenMaXwell does not differentiate between HE and EH waves.
Press the Read… button to read project data from a file. A file name dialog will allow you to select a file name. OpenMaXwell will not only read the project file, but also all associated data files, i.e. files with the same name, but a different extension.
Press the Write… button to write project data to a file. A file name dialog will allow you to select a file name to write to. OpenMaXwell will not only save the Project dialog data in the project file, but it will also save all of the data of the associated dialogs in files with the same name, but different extensions. Note that for files that consume large amounts of memory only the headers will be saved, for example the Function file, the Field file, and the MMP file. The function values, field values, and the MMP matrices will not be saved however.
Press the Close button to close the dialog. Note that the data in the dialog becomes effective once the dialog is closed.
Responsible for this web page: Ch. Hafner, Computational Optics Group, IEF, ETH, 8092 Zurich, Switzerland
Last update
17.02.2014