2D points 3D Objects 3D Points Boundary Cursor position Data for selected object Domain Expansion Field Field components Field formula Field tubes Function Generate expansions along 2D boundary Generate expansions for 3D objects Grid formula Grid transformation Info and movie directives Insert Integral Modify 2D expansions MMP Movie Open GL window PET basis PFD (predefined FD) Project Space, plane, arrow, or point Tools and draw Transformation data Window
Press the function button ![]() or
select Function... from the Tools menu to
open this dialog.
or
select Function... from the Tools menu to
open this dialog.
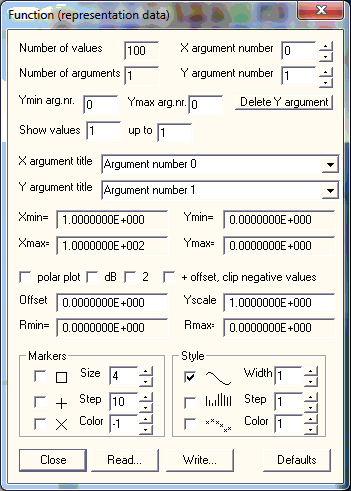
Note: The Ymin arg.nr. and Ymax arg.nr. boxes in this dialog are not used in the current implementation of OpenMaXwell.
To store a simple real valued function of a real valued argument one usually uses two arrays. For example, the array F(k) stores the function values and X(k) stores the corresponding values of the arguments. Instead, one can pack F and X in a single array A that corresponds to a matrix with two columns. One then has A(1,k)=F(k) and A(2,k)=X(k). This packed array storage can be used for more complicated situations. For example, one can have A(1,k)=Real(F(k)), A(2,k)=Imag(F(k)), A(3,k)=Real(X(k)), A(4,k)=Imag(X(k)) when one wants to store a complex function with a complex argument. Another example is the storage of a real function F with two arguments X and Y. Here, one can write A(1,k)=F(k), A(2,k)=X(k), A(3,k)=Y(k). In general, each column of the matrix A can either correspond to an argument or to a function. OpenMaXwell uses this packed array storage. Therefore, OpenMaXwell can store several real valued functions of one and the same real argument or a real valued function of several real arguments, etc. It stores all functions and arguments in an array with n columns and an arbitrary number of rows. The columns contain the data of the functions or arguments, the rows contain the corresponding values. OpenMaXwell does not ‘know’ which of the columns contains an argument and which contains a function. Therefore, all columns are called ‘argument’ and it is assumed that the user knows when an ‘argument’ is in fact a function.
OpenMaXwell counts the number of arguments and the number of values, i.e., the number of columns and rows, and displays these numbers in the corresponding boxes.
When a simple, real valued function F(X) is sampled in an equidistant set of points, you might wish to store the function values only. In this case, the array A that stores the function has only one column: A(1,k)=F(k). To plot such a function, the information of the argument X is missing. Instead of F(X) you can still plot F(k). The row number k is used when you specify the argument number 0. This is useful, for example, when you store results of an iterative process in the function array. The iteration number need not be stored explicitly, because it corresponds to the row number k.
OpenMaXwell can draw an XY plot, where X is the horizontal and Y the vertical direction on the screen. Any of the ‘arguments’ (or functions) can be displayed either in X or Y direction. You select this in the argument number boxes.
The X and Y values of the function to be drawn are stored in the function array, which has N rows, where N is specified in the Number of values box. If you wish to plot only a part of the function, you may select the minimum and maximum row numbers used for drawing in the Show values ... up to ... boxes.
The range of the X and Y arguments is displayed in the Xmin, Xmax, Ymin, Ymax boxes. This information is useful for selecting appropriate borders of the graphic window.
The argument title boxes specify the labels for the X and Y axes respectively and are displayed along with the function representation.
Although OpenMaXwell draws only one function at a time, you can repeat this procedure to obtaining several functions on the screen. To differentiate between the different functions OpenMaXwell provides three markers. These markers can be sized by specifying their size in pixels and their color set by selecting any of the available color numbers. Markers can be set for the values 1, n+1, 2n+1. The step n can be defined in the corresponding box.
OpenMaXwell offers three line styles for drawing functions. Moreover, you can set the line width (in pixels) and color numbers for drawing in the corresponding boxes. If the function has a large number of values, you may wish to get a quick overview without drawing every value. To do this specify a step size n in the corresponding box and OpenMaXwell will draw the function only for the values 1, n+1, 2n+1,…
Press the Read… button to read function data from a file. Since a function file can contain the function representation data defined in this dialog and/or the values of the function(s) , OpenMaXwell will ask you first, which portion of data you want to read. For security reasons, OpenMaXwell asks you if you want to overwrite the original function(s). Afterwards, a file name dialog will allow you to select the file to read.
OpenMaXwell allows you to append the data in the function file either as new columns or as new rows of the function array. It will ask you what you want if you answer the question "Overwrite functions?" in the negative.
Press the Write… button to write function data to a file. Since a function file can contain the function representation data defined in this dialog and/or the values of the function(s), OpenMaXwell will ask you first, which portion of data you want to save. Afterwards, a file name dialog will allow you to select the file name to save the data to.
If you have modified some data and wish to obtain the default settings again, press the Default button.
You may represent functions by polar plots, when you turn the polar plot check box on. Then, the X argument will be interpreted as angle (in degrees) and the Y argument will be interpreted as distance r from the origin.
When you turn on one of the following check boxes, the y values will be pre-processed as follows:
dB evaluates 10*log10(y) instead of y.
2 computes the square of y.
+ offset, clip negative values: the offset value specified in the Offset box is added to y, i.e. y+offset is displayed rather than y. Furthermore, values that are still negative will be set equal to 0. This is especially important for polar plots that look strange when y is negative.
Note: when dB and 2 are checked simultaneously, you obtain 10*log10(y*y)=20*log10(y).
Sometimes, it is convenient to scale the Y argument before plotting. This is done, when you specifiy a value different from 1 in the Yscale box. In order to simplify the selection of the scaling factor, the current minimum and maximum y values (r values in the case of polar plots) are displayed in the Rmin= and Rmax= boxes respectivey. Note that the values in these boxes are not refreshed when you modify Offset or Yscale. In order to refresh these values, you may click, for example, polar plot twice.
Press the Close button to close the dialog. Note that the current data in the edit boxes become effective once the dialog is closed.
Responsible for this web page: Ch. Hafner, Computational Optics Group, IEF, ETH, 8092 Zurich, Switzerland
Last update
03.07.2014